Constrained multinomial stick-breaking

Multinomial stickbreaking is an easy

Code

sigmoid <- function(x){1/(1 + exp(-x))}

tilde_pi2pi <- function(tpi){
  tmp <- c(1, head(cumprod(1 - tpi), -1))
  pi <- tmp * tpi
  pi <- c(pi, (1 - sum(tmp * pi)))
  return(pi)
}

make_pi <- function(K, b0, b, x){
  psi <-  do.call(cbind, purrr::map(b0, ~b + x + .x))
  tilde_pi <- sigmoid(psi)
  tpi <- tilde_pi[12, ]
  pi <- do.call(rbind, purrr::map(1:nrow(tilde_pi), ~tilde_pi2pi(tilde_pi[.x,])))
  return(pi)
}

plot_pi <- function(pi, idx, x){
  par(mfrow = c(1, length(idx)))
  K <- ncol(pi)
  for(i in idx){
    plot(1:K, pi[i,], type = 'b', xlab = 'K', ylab = 'prob', main=paste0('x = ', x[i]))
  }
}

Shared

\(\psi_k \equiv \psi\; \forall\ k \in[0, K-1]\)

Code

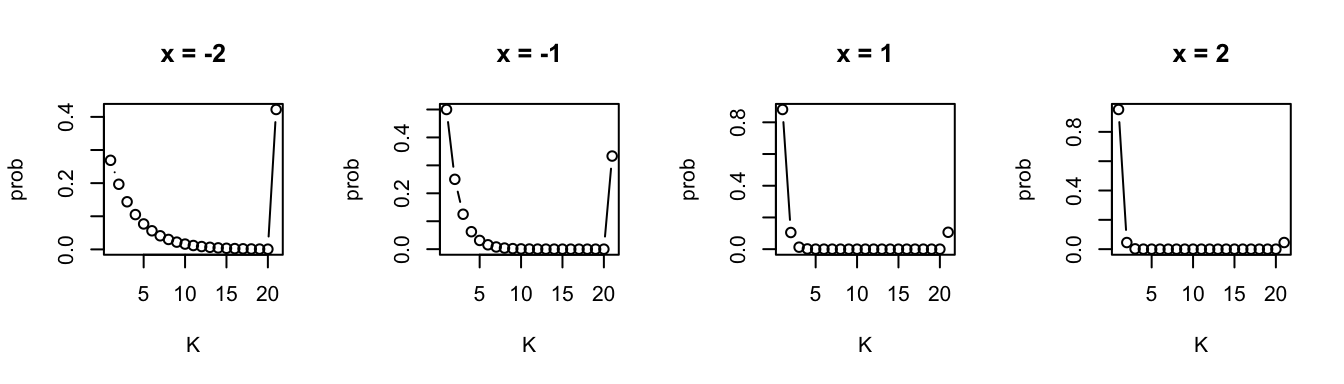
K <- 20
b0 <- rep(0, K)
b <- 1
x <- seq(-3, 3.2, by=0.2)
pi <- make_pi(K, b0, b, x)
plot_pi(pi, c(6, 11, 21, 26), x)

Fixed prediction, seperate intercept

Code

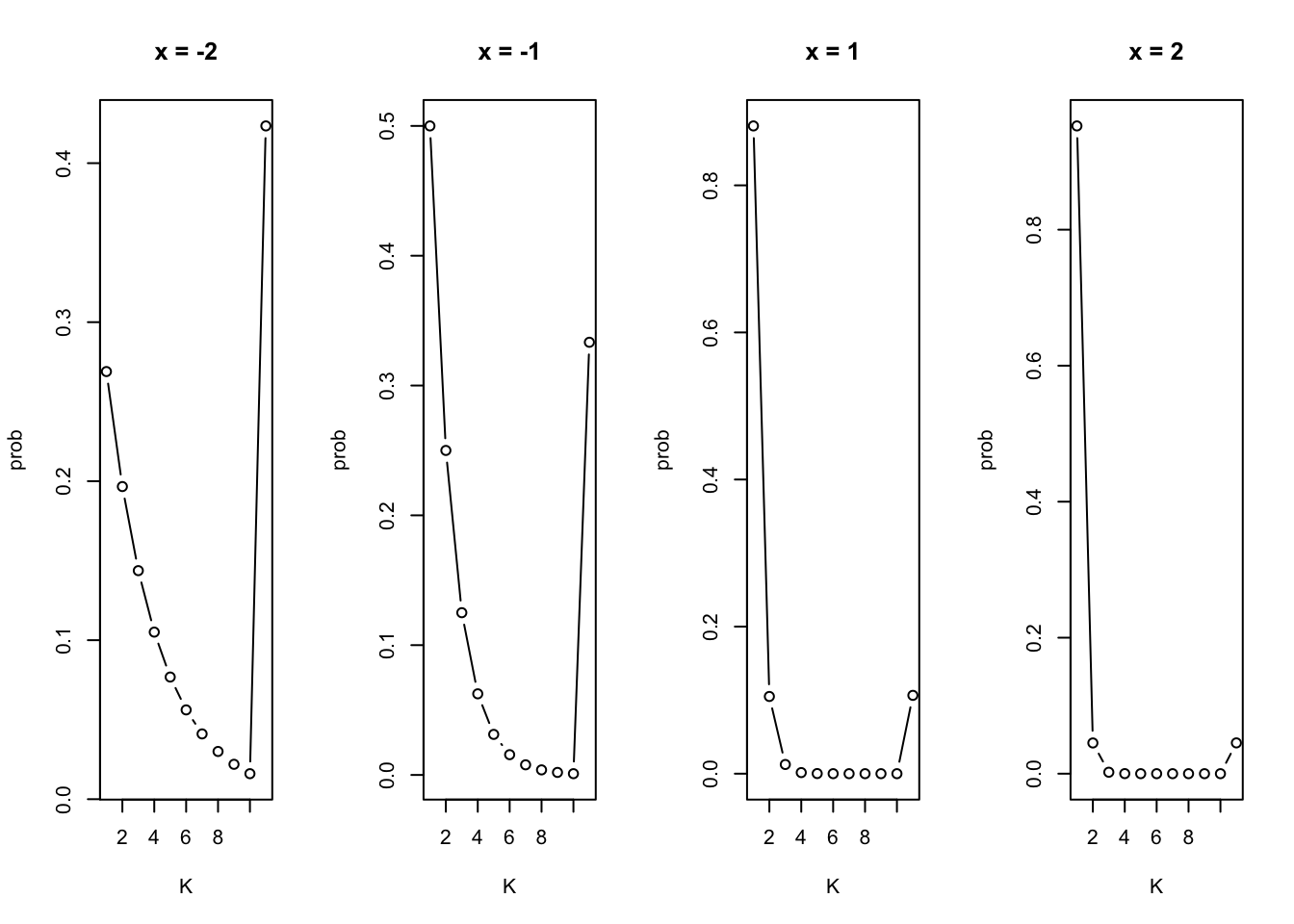
K <- 10
b0 <- rep(0, K)
b <- 1
x <- seq(-3, 3, by=0.2)
pi <- make_pi(K, b0, b, x)
plot_pi(pi, c(6, 11, 21, 26), x)

Code

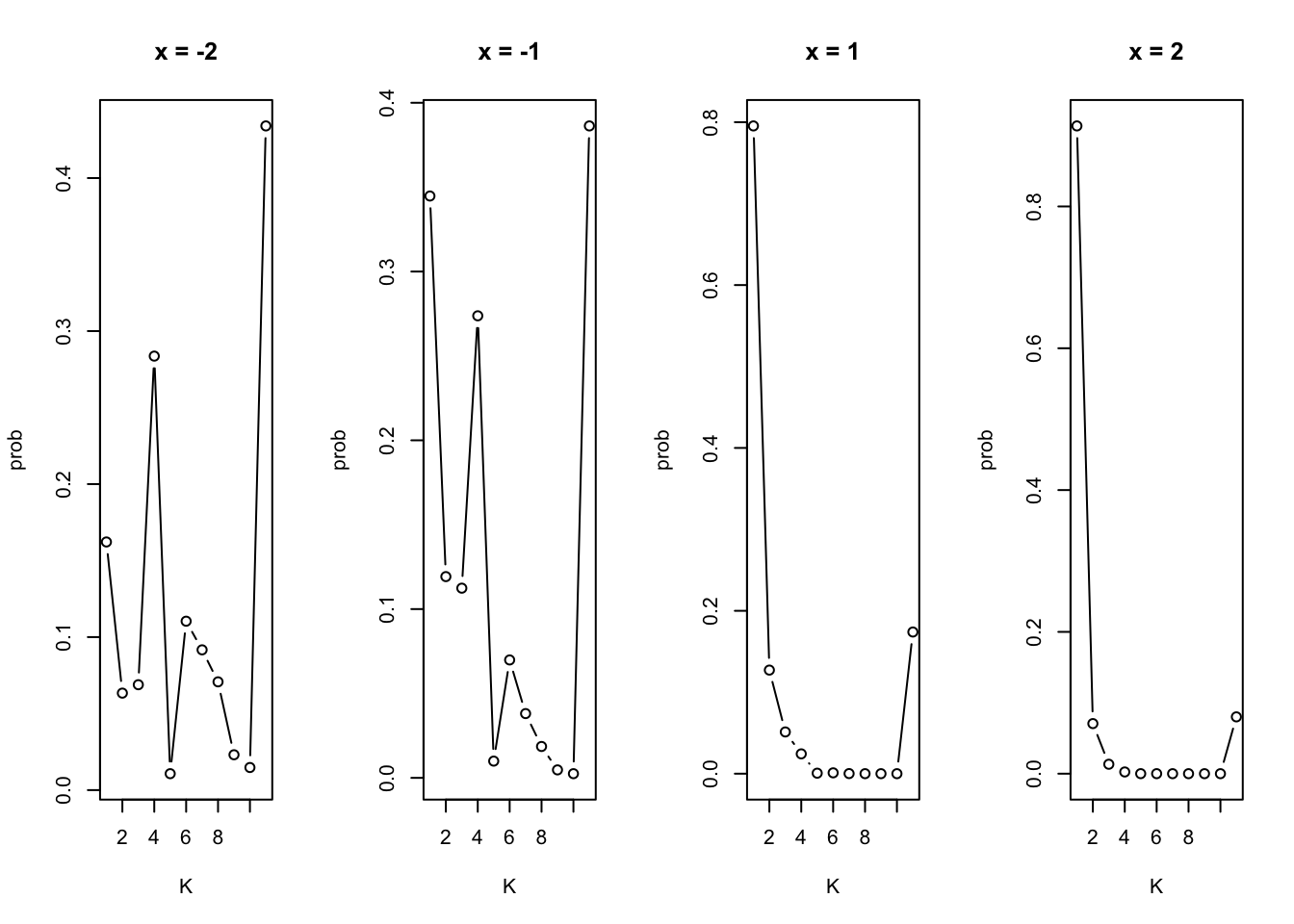
K <- 10
b0 <- rnorm(10)
b <- 1
x <- seq(-3, 3, by=0.2)
pi <- make_pi(K, b0, b, x)
plot_pi(pi, c(6, 11, 21, 26), x)

Code

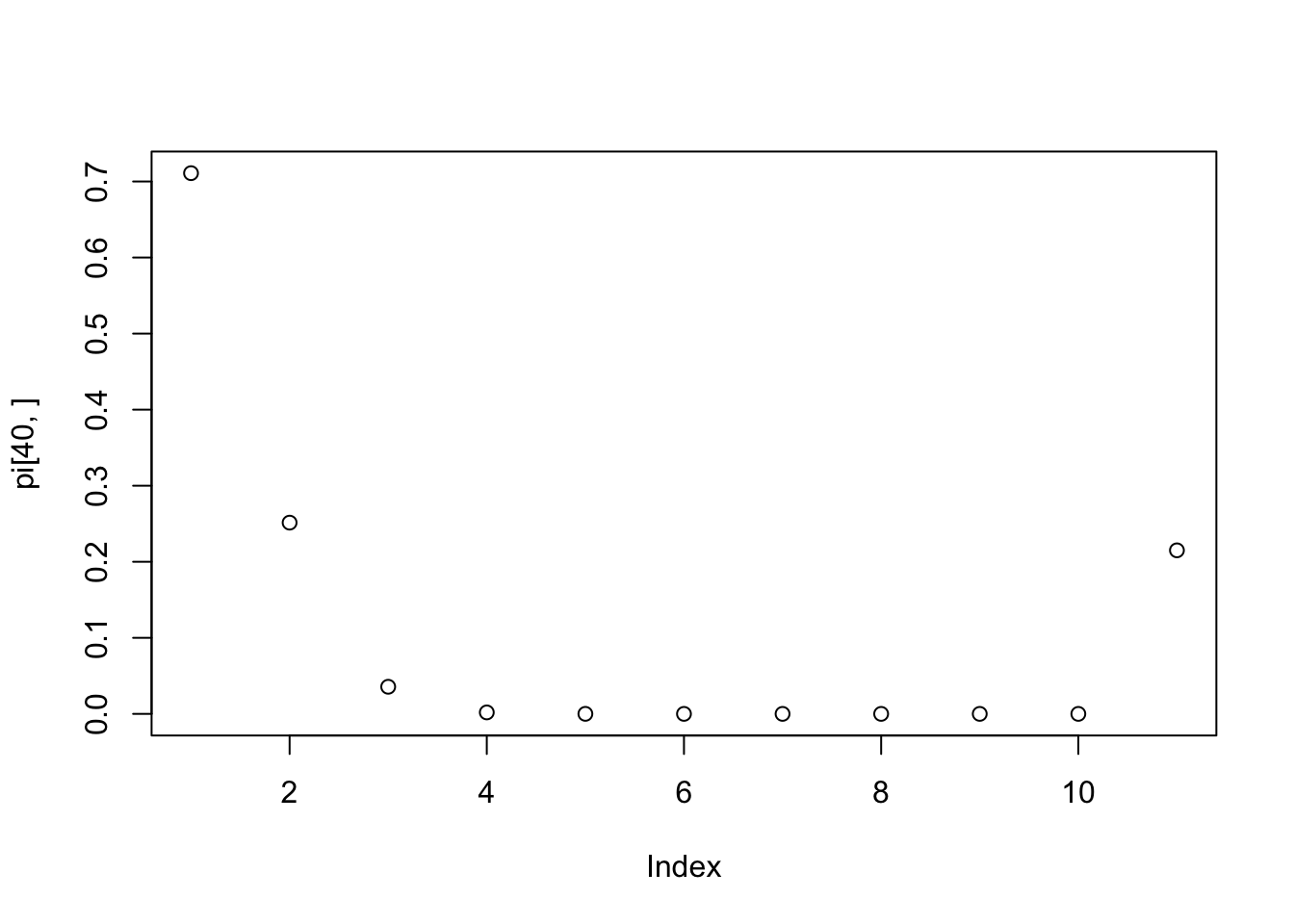
K <- 10
b0 <- 1:K
b <- 1
x <- seq(-5, 5, by=0.1)
pi <- make_pi(K, b0, b, x)
plot(pi[40,])

Code

K <- 10
b0 <- rnorm(K)
b <- 1
x <- seq(-5, 5, by=0.1)
pi <- make_pi(K, b0, b, x)

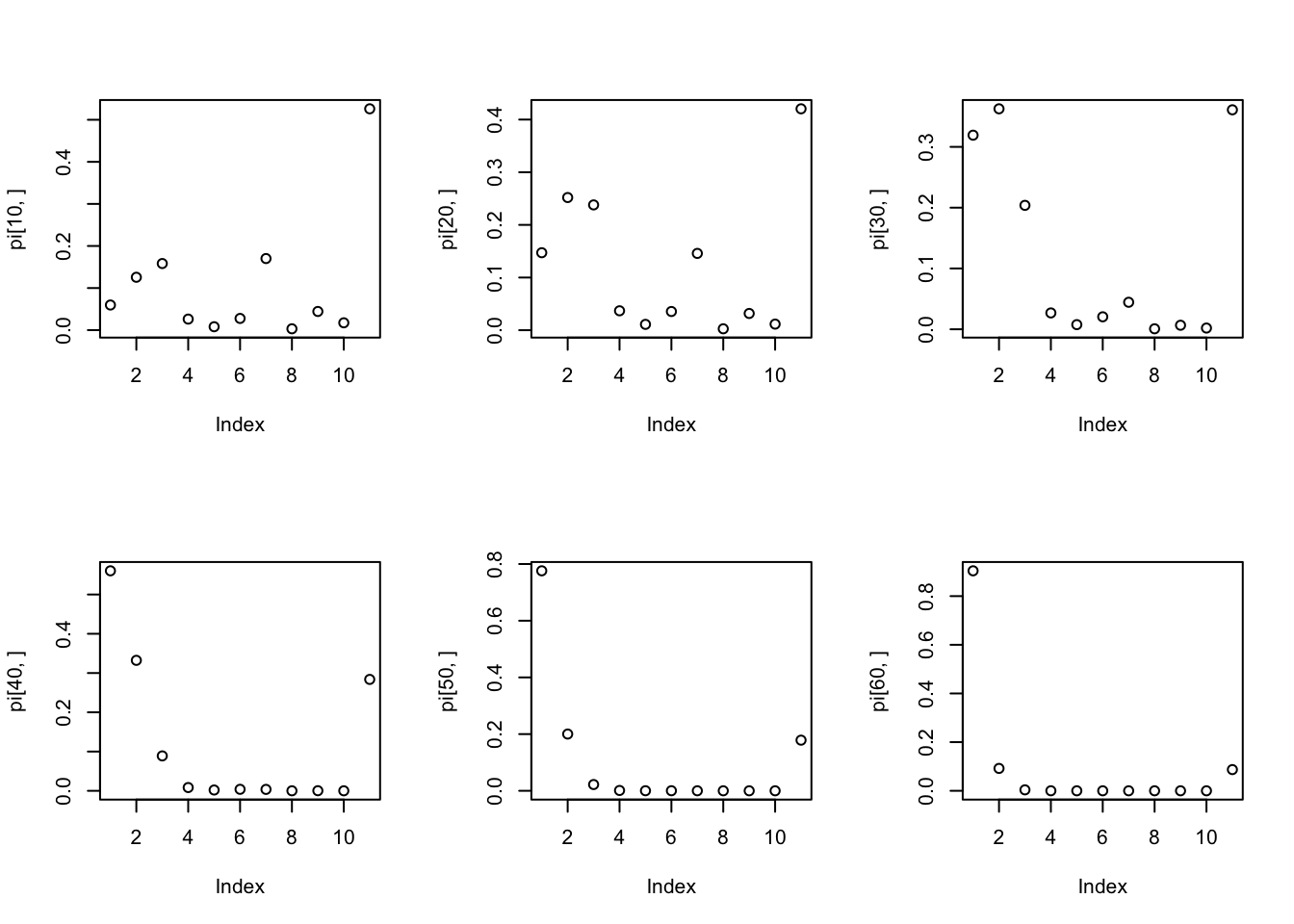
par(mfrow = c(2, 3))
plot(pi[10,])
plot(pi[20,])
plot(pi[30,])
plot(pi[40,])
plot(pi[50,])
plot(pi[60,])