Another Generalized SuSiE presentation
Overview
- Publication plan:
- Generalized SuSiE via IBSS, emphasis on fine-mapping for non-Gaussian models
- GSEA with logistic SuSiE
Fine-mapping under the multivariate Gaussian model
Most fine-mapping methods assume summary statistics from marginal association studies are normally distributed, with covariance determined by LD 1
\[\begin{align*} \hat{ {\bf z} } \sim N({\bf z}, R) \end{align*}\]
Statistical property of OLS– what if the marginal effects are coming from somewhere else?
What do we want to accomplish?
- Establish when there is a problem with fine-mapping with summary stats from non-Gaussian models
- (Hopefully) find that these situations are not uncommon
- (Hopefully) demonstrate that GIBSS offers improvement in these situations
- (Fallback) advise people to fine map with summary statistics from linear models
Three horse race
| Method | Notes | Summary stats |
|---|---|---|
| Generalized IBSS | “correct” model, hueristic algorithm | No |
| Logistic + RSS | ad-hoc, actually used (5,6) | Yes |
| Linear + RSS | mis-specified model, correct algorithm | Yes |
GIBSS overview
- Compute univariate effect estimates using regression of choice, must return MLE and stderr
- Compute/approximate BFs and posterior means: Laplace, quadrature, etc.
- Use predictions as fixed offsets when updating next effect
- Iterate until
convergence(we don’t know if it converges)
Key questions
- Generalized IBSS vs Logistic RSS
- \(L=1\) case reduces to IBSS-Laplace vs IBSS-ABF
- GIBSS-Laplace should be strictly better, but by how much, and when?
- \(L > 1\) all bets are off with Logistic RSS
- Linear SuSiE vs Logistic RSS
- Helpful to look at \(L=1\) case, Linear + Wakefield vs Logistic + Wakefield
- In GWAS linear regression is often a good approximation to logistic regression
- Linear SuSiE vs Generalized IBSS
- When does linear SuSiE give reliable results?
- When does GIBSS provide and advantage?
Potential problems
Logistic + RSS
- Covariate of marginal \(z\)-scores do not correspond with LD
- Under appreciated source of “LD Mismatch?”
- Follow-up: what is the correct covariance matrix?
- Inherits problems from using ABF– not the most accurate
Logistic GIBSS
- Marginal effect estimates are biased when there is a large genetic component
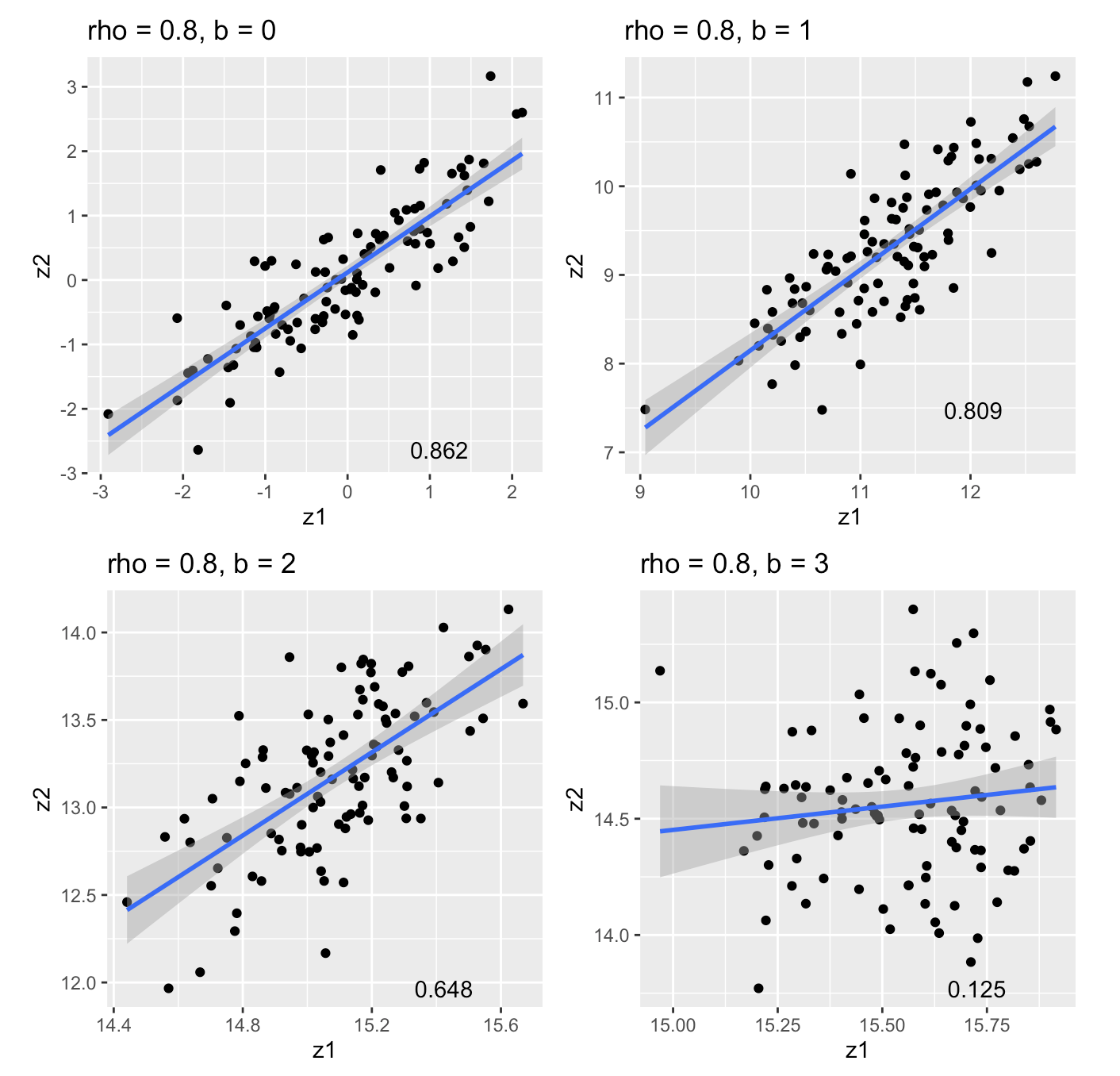
Correlation of marginal effects in logistic regression:
- Simulate \(\begin{bmatrix}x_1 \\ x_2 \end{bmatrix} \sim N(\begin{bmatrix}0 \\ 0 \end{bmatrix}, \begin{bmatrix}1 & \rho \\ \rho & 1 \end{bmatrix})\)
- Simulate \(y\) under a logistic model \(y \sim Bin(1, \sigma(\psi)), \; \psi := b_0 + b x_1\)
- \(cor(z_1, z_2) \neq \rho \implies\) LD matrix is the wrong covariance matrix
Correlation of marginal effects (cont)
An under-appreciated source of “LD mismatch”?
\(n = 500\), \(b_0 = -1\), \(b = 0, 1, 2, 3\) 1
Laplace vs Wakefield (Review)
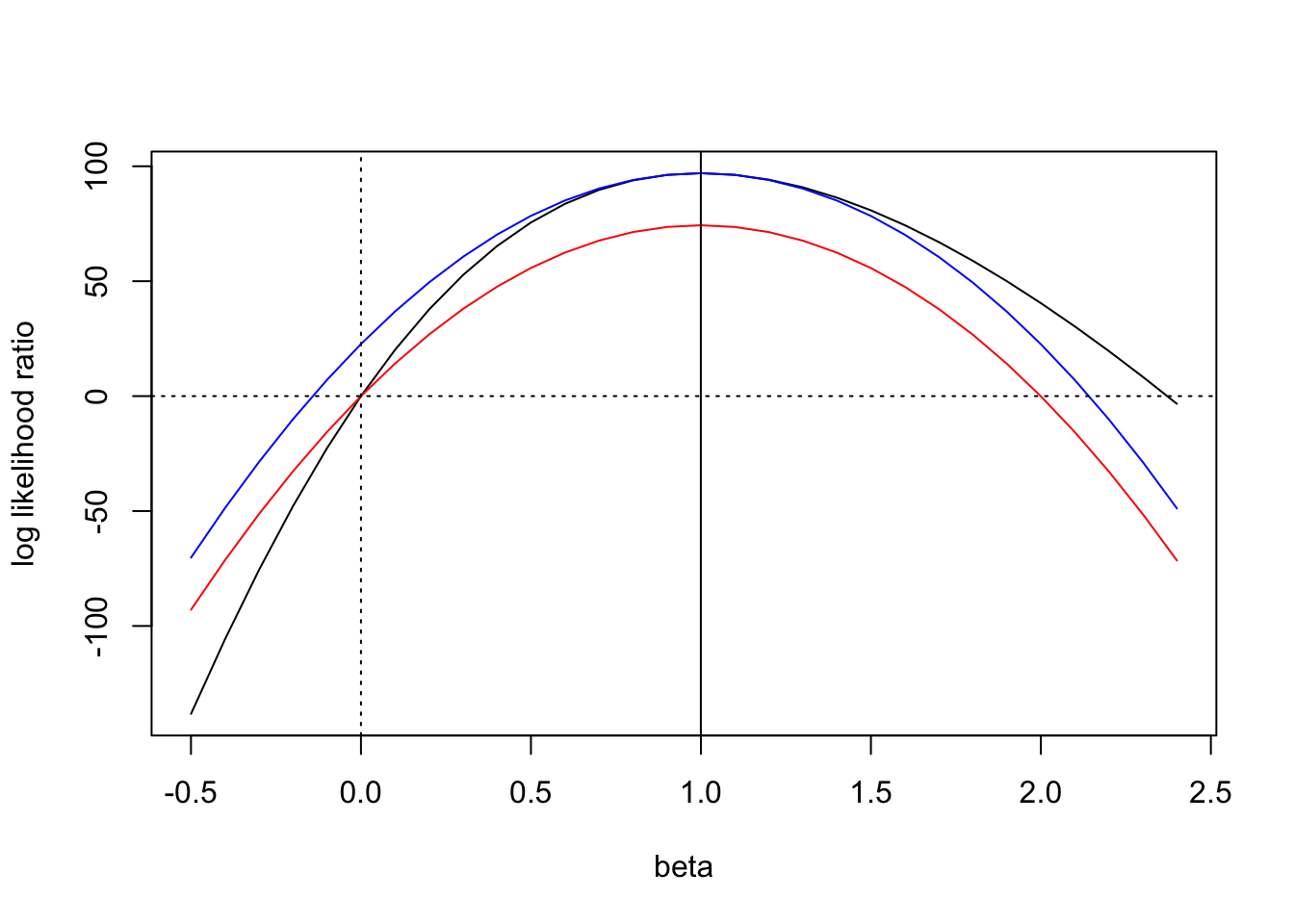
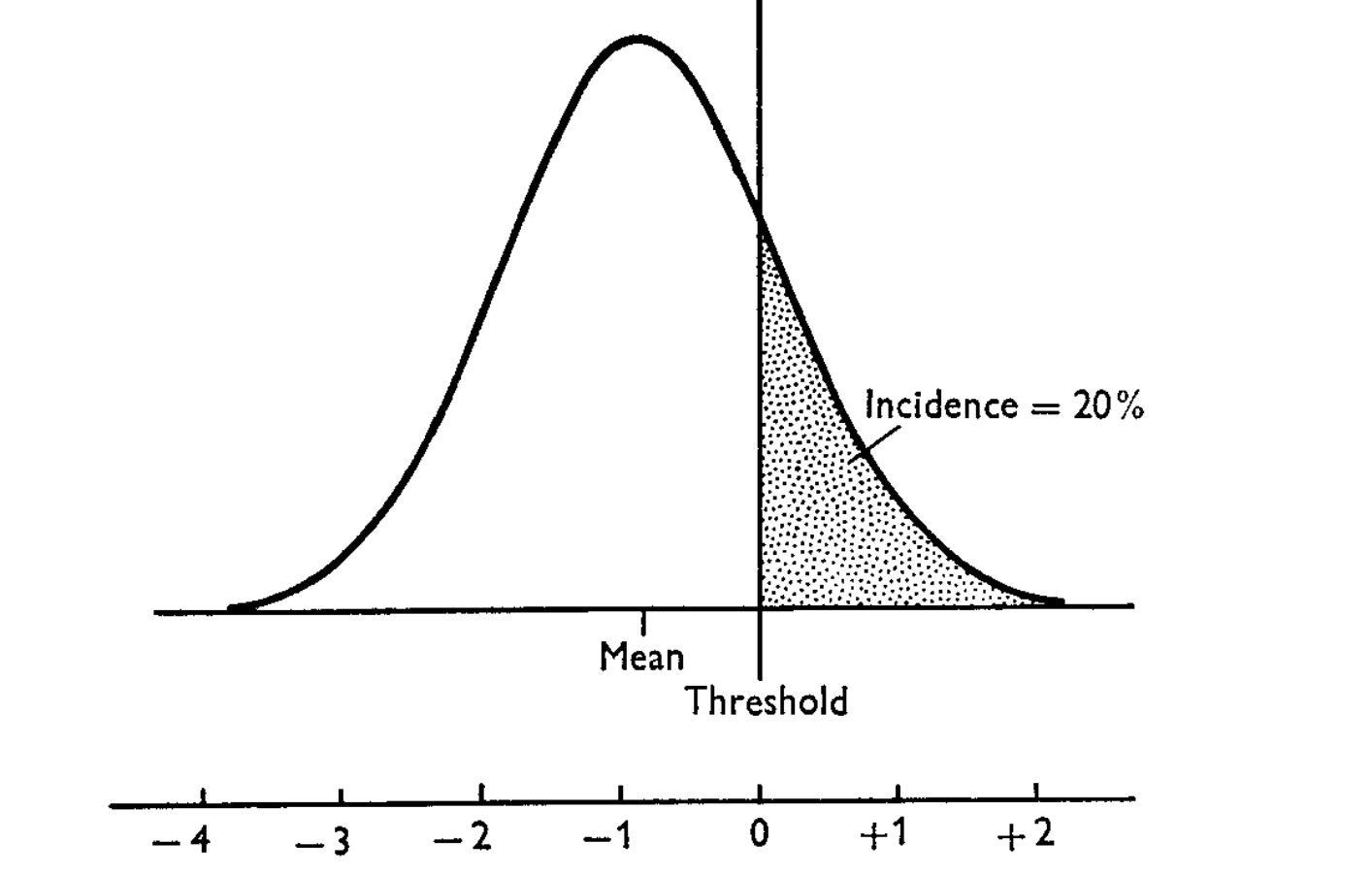
Figure 1: Wakefield’s ABF can be order of magnitude off when the \(z\)-score is large
Problems with Wakefield (Review)
!()[resources/abf_biased.png]
!()[resources/abf_eq.png]
SuSiE-RSS and the Wakefield BF
- Recall that Wakefield’s ABF is not accurate when the \(z\)-score is large
- Applying SuSiE-RSS to summary statistics from some other model besides Gaussian linear model
How large do the \(z\)-scores need to be?
Biased effect estimates (and BFs)
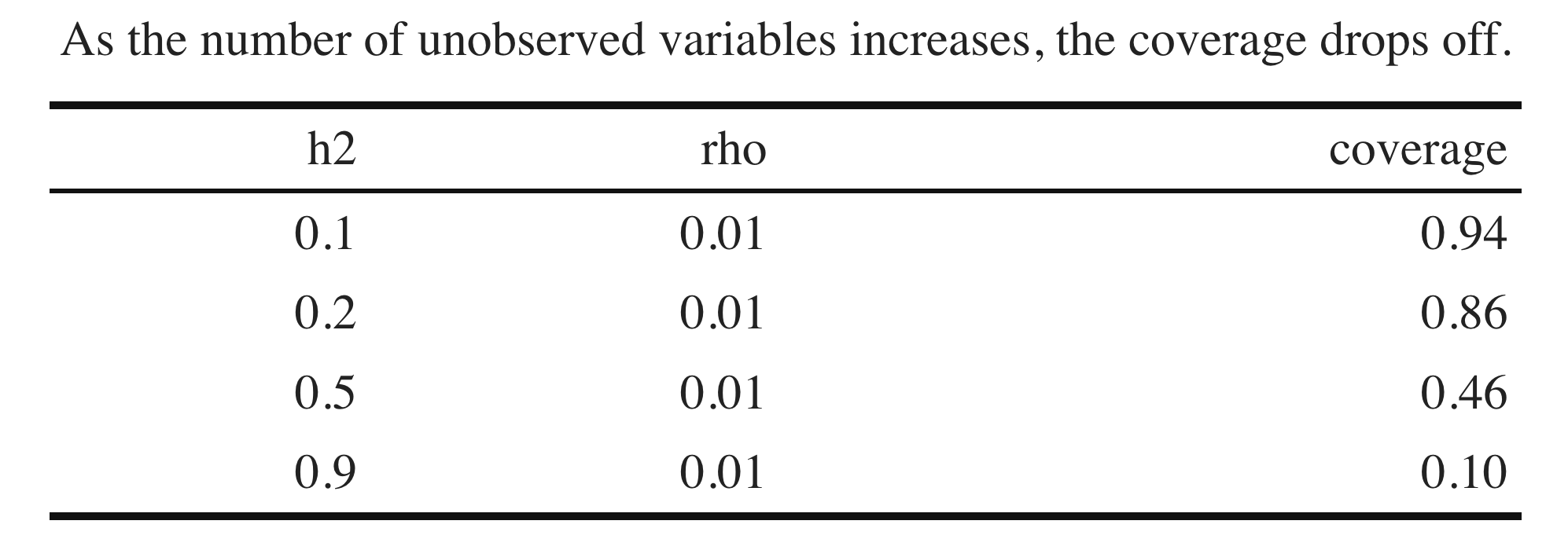
Simulation: one causal variant in the locus that explains \(1\%\) of heritability of liability. \(h^2 = 0.1, 0.2, 0.5, 0.9\)
\[\begin{align*} y \sim Bin(1, \sigma(\psi)) \\ \psi = b_0 + b x + \epsilon \\ \epsilon \sim N(0, \sigma^2) \end{align*}\]
Biased effect estimates (and BFs)
Biased effect estimates (and BFs)
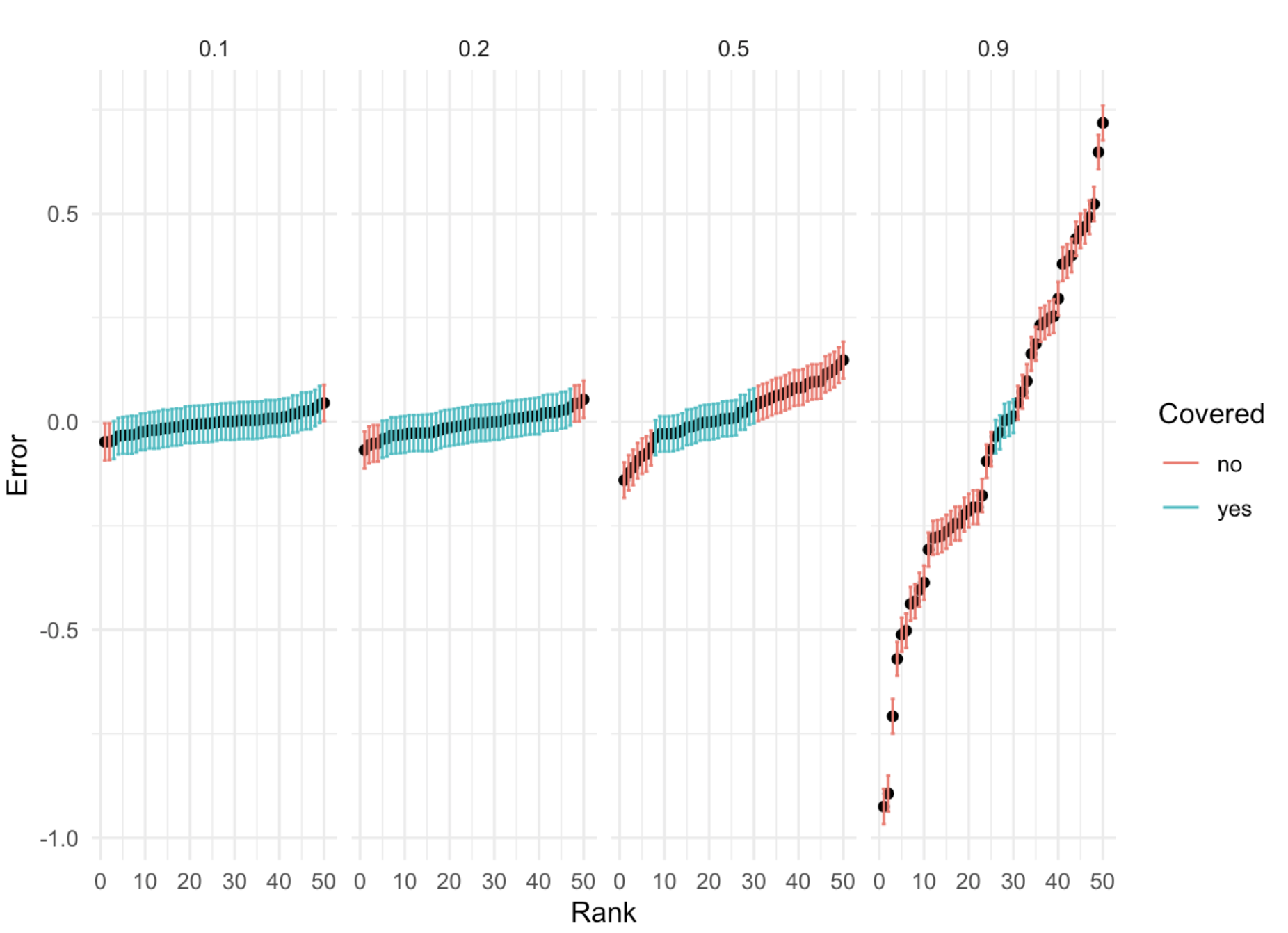
95% C.I. for different \(h^2\)
Biased effect estimates (and BFs)
- For phenotypes with substantial \(h^2\) of liability, restricting our attention to a single locus will lead to biased effect estimates
- Remark: linear model doesn’t struggle with this issue because in practice we estimate the residual variance (or set conservatively)
- Remark:basically a random intercept model, but this seems a little different than the usual motivation for mixed model approaches.
Real data analsis
- Q: if we reun SuSiE, GIBSS, Logistic + RSS on real case-control GWAS do we get qualitatively different results?
- Don’t know ground truth, hard to tell what is performing better
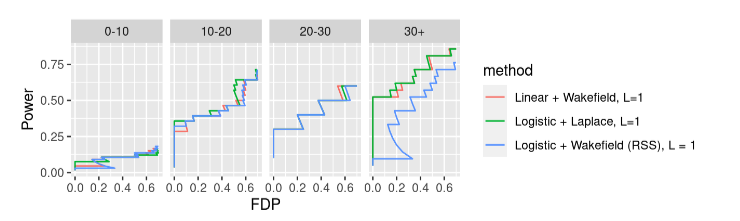
- Replication failure rate (RFR) among PIPs proposed in (7) may support claim that using GIBSS > Linear + RSS > Logistic + RSS
- Other ideas?
- Do you know of imbalanced case-control GWAS, survival GWAS, etc. GWAS on count based phenotypes, etc to test out?
Simulation
\[ \begin{align*} y_i &\sim Bin\left(1, \sigma \left(b_0 + \sum_{j=1}^q b_j x_{ij} + \delta\right)\right)\\ b &\sim N(0, \sigma^2) \\ \delta &\sim N(0, \nu - q \sigma^2)\\ \end{align*} \]
| Value | Description |
|---|---|
| \(X\) | Standardized genotypes |
| \(\sigma^2\) | Variance of standardized effects, i.e. \(b \sim N(0, \sigma^2)\) |
| \(q\) | Number of causal variants in locus |
| \(\rho\) | Fraction of variance of genetic component in-locus |
| \(k\) | Fraction of cases (determines \(b_0\)) |
| \(q\sigma^2\) | (Expected) variance of genetic component in-locus |
| \(\nu\) | \(q \sigma^2/\rho\), (expected) variance of genetic component |
| \(h^2\) | \(\nu / (\nu + \pi^2/3)\), (expected) heritability of liability 1 |
Examples where SuSiE is applied to non-Gaussian linear summary stats
(5), Alzheimers meta analysis combining linear and logistic association studies (6) logistic-mixed model SAIGE + SuSiE
When does Logistic + Wakefield perform poorly?
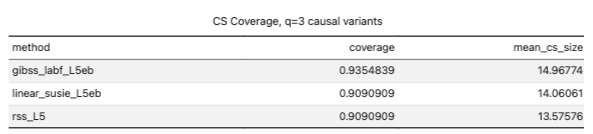
- accidentally wiped the simulations, need to regenerate
- apparently
Dealing with intercept + covariates
A few options:
- Estimate in outer loop, treat as a fixed offset while estimating SERs
- Re-estimate covariate effects for each variable
- Found that reestimating intercept was helpful
Univariate BF
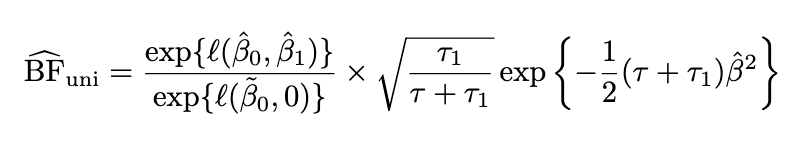
Limiting BF
Limiting BF
Idea put a normal prior on all covariates \(\begin{bmatrix} \alpha \\ \beta \end{bmatrix} \sim N(\begin{bmatrix} 0 \\ 0 \end{bmatrix}, \begin{bmatrix} I_{p-1} \tau_0^{-1} & 0 \\ 0 & \tau_1^{-1} \end{bmatrix}\) and compute Laplace approximation to the BF. Take \(\tau_0 \rightarrow 0+\).
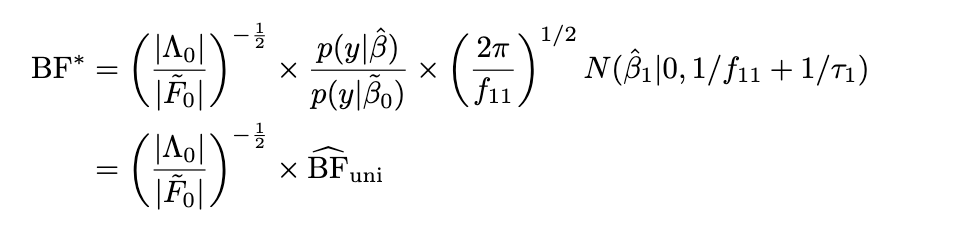
Q: How variable is the scaling factor? Can we get away with just using the univariate BF?
Better quadrature rule
Gauss-Hermite quadrature
\[ I = \int f(x) e^{-x^2} dx \approx \sum_{i=1}^n w_i f(x_i) \]
\((x_i)_{i=1}^n\) are the roots of the Hermite polynomial \(H_n(x)\), \(w_i = \frac{2^{n-1} n! \sqrt{\pi}}{n^2 H_{n-1}^2 (x_i)}\)
\[ I = \int f(x) dx = \int \left[\frac{f(x)}{q(x)} \right] q(x) dx, \;\; q(x) = N(x | \mu, \sigma^2)\; \text{s.t.}\; \frac{f}{q} \approx 1 \]
- Asymptotically correct
- Otherwise, integrating a function with little variation where the integrand has mass
- Upshot: very accurate integrals with e.g. \(n = 8, 16\).
(note: change of variable + scaling factor to apply the \(n\) point Hermite quadrature rule)